2020年网络科学的4个前沿方向:从时序网络到高阶网络 李静林 2020-03-31 23:03 No Comment 3130次浏览 # 2020年网络科学的4个前沿方向:从时序网络到高阶网络 [转载](https://www.toutiao.com/i6799444117022573060/) 集智俱乐部 2020-03-02 11:15:50 # **导语** 网络科学著名学者梅森·波特近期在一篇综述中,介绍了时序网络、网络动力学过程、自适应网络和高阶网络这四个2020年网络科学的研究热点。本文将对这篇综述做简介,并推荐部分相关论文。  网络科学日新月异,在新的一年中,有哪些最新的研究方向?曾获网络科学大会ER奖的加州大学洛杉矶分校数学教授Mason A. Porter,近期在 arxiv.org 提交了一篇综述论文 Nonlinearity + Networks: A 2020 Vision,指出了未来复杂网络研究的四个热点,分别是: 1.时序网络(temporal networks)2020网络科学的4个前沿研究方向 2.网络上的动力学过程 (dynamical processes on network) 3.自适应网络(adaptive network) 4.高阶网络(high order network) > 论文题目: Nonlinearity + Networks: A 2020 Vision > > 论文地址: https://arxiv.org/abs/1911.03805 本文将简单介绍这四个前沿领域及其进展,对网络科学感兴趣的研究者,想要跟上时代快些上车吧。 # **1. 时序网络 temporal networks** 网络不是一成不变的,去年你的朋友圈中活跃的人,在今年不一定活跃。时序网络中的边,会随着时间的变化出现或者消失。下图对比了普通的网络(左边)与时序网络(右边)的不同。 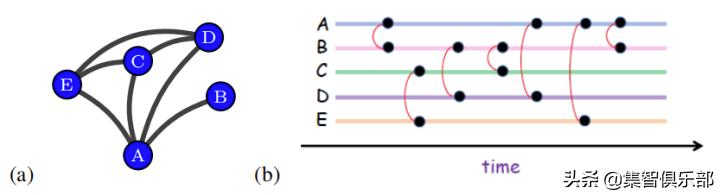 图 1:时序网络随时间展开图 如果时间是离散化表示的,则可以用多层网络(multi-layer network)来表示时序网络,如下图所示: 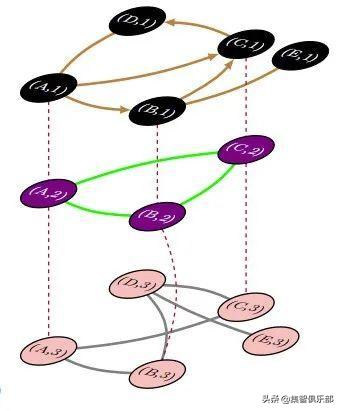 图 2:多层时序网络示意图,图中的每一层代表一个时间点 时序网络的多层表示,还促进了对网络上社区发现(community detection),以及社区合并、分离及演进的研究。如今时序网络上的社区发现方法,已经在神经、材料、疾病传播、生态、投票等多个场景下得到了成功的应用。 另一种描述时序网络的方法是Activity-driven,即AD 模型。AD 模型可以用节点的激活概率(activity potential)函数,来描述时序网络中节点之间的连接方式和相互作用,也就是网络上的动力学。 节点的中心度(centrality)是长期的研究热点,这一指标可以揭示网络中节点的角色,例如网页排名、学术评价。近年来,各种类型的节点中心度,包括介度中心度、连通度、特征向量中心度等,已经被推广到了时序网络上,来衡量节点的重要性如何随网络结构改变而变化。 在2020年1月的一篇关于时序网络动力学的研究中,研究者。针对不同场景下,面对面交流时呈现出的模式,通过优先激活( preferential activation)模型,可以拟合在学校,医院等不同环境下,人与人进行交流时的时序网络所呈现的特征。研究者发现,当节点之间相互作用可以受到环境影响时,环境变化对时序网络的动力学行为有重要影响。 > 论文题目: Impact of environmental changes on the dynamics of temporal networks > > 论文地址: https://arxiv.org/abs/2001.02847 2019 年 12 月一篇关注时序网络动力学的 arxiv 文章中,作者提出能够对网络中的连边之间的竞争和相关性进行建模的方法。通过模型,可以模拟在边和节点演化动力学中,满足长尾分布的时序网络。 > 论文题目: Modeling temporal networks with bursty activity patterns of nodes and links > > 论文地址: https://arxiv.org/abs/1912.11212 # **2. 网络上的动力学dynamical processes on network** 节点之间的互动机制,被称为网络中的动力学。网络上节点的互动,或是按照固定的规则,或是在决定是否行动时会引入随机性。当节点的互动导致网络中的边消失或生成时,就会产生时序网络。通过在网络中引入反馈,网络上的动力学可以确定复杂性的成因,只有同时具有正反馈和负反馈,且两者的比例处在临界值时,系统才会产生并维持复杂性。未来的网络动力学前沿,聚焦在多层网络(multi-layer)和度量图(metric graphs)两个子领域。 在多层网络上研究动力学过程,可以有两种思路,一种是同样的互动机制作用于不同层的网络,另一种是不同层的网络采用不同的互动机制。例如模因(meme),可以在微信、微博、B 站等多个社交媒体上传播,它们组成了多层网络。一方面,模因在这些网络上的传播过程,有着相似的动力学机制,不同的社交媒体在网络结构上会有不同,这带来模因传播速度和程度的差异。另一方面,模因还可以在线下真实的人群中,通过口耳相传进行,这时就需要使用不同于线上的传播机制来进行建模。 推荐阅读:科学玩“梗”:模因(meme)如何在社交网络中传播? 相比一般的网络,Metric graph除了节点和节点之间的连接,每个节点还包含一个正数,称为该边的长度,可以理解为该点的“能力”。如果把节点看成是大海中的一条条船,将节点的长度看成是距离海平面的高度,则可以研究metric graph的波动。对于粗粒度材料中的波动扩散(wave propagation in granular materials)或者城市交通中的车流量,Metric graph是很自然的一种建模方法。 Explosive phenomena in complex networks 探讨网络中的爆发式行为,是网络中动力学的研究的一个具体案例。 推荐阅读:复杂网络上的爆发现象综述:相变、爆发、生命起源有何共同之处 # **3. 自适应网络 adaptive network** 将自适应网络与之前谈到的网络动力学区分开的是前者关注的节点间的共同进化,即节点本身会随着局部的网络结构变化,而改变自己与其他节点的交互模式,而不只是改变节点的连接或metric。扩展来看,自适应网络考察的是节点间的博弈如何节点间的合作,以及群体智慧的涌现。 自适应网络的建模,常常关注节点在何时会rewire,例如Gross提出的疾病传播模型,节点会以一定概率切断和已感染节点的连接,并和未感染的节点建立连接,已保护自己。或者在社交网络上,选择与那些观点和自己相近的节点连接,并取关那些观点或阅读难度和自己差距较大的媒体。自适应网络可以解释为何由普通人构成的网络中会出现极端思想等反直觉的现象,之前报道过的一个自适应网络的例子是“删贴对打击极端思想无效”节点间的震荡耦合(coupling between oscillators)与同步,是自适应网络的另一个研究热点。 关于社交网络中,如何通过积极的寻找其他成员,通过改变他们的观点来改变网络中的流行观念,且通过最少的人数,获取最大的影响力19年的论文中给出了对应的模型。 > 论文题目: How does active participation effect consensus: Adaptive network model of opinion dynamics and influence maximizing rewiring > > 论文地址: https://arxiv.org/abs/1906.00868 在社交网络上,回音室(echo chamber)效应指相同观点的人通过自我选择,看相同政治观点的内容,最终具有相近的,同时更极端的政治光谱。下面这篇论文中针对这一现象,建立自适应网络模型,通过模拟数据,该模型可以对如何传播想要传播的信息,或者阻断不想要传播的信息,提供指导。 > 论文题目: A Model for the Influence of Media on the Ideology of Content in Online Social Networks > > 论文地址:https://arxiv.org/abs/1904.09238 # **4. 高阶网络 high order network** 传统的网络只考虑两个节点之间的关系,但是对于现实情况,往往是多个节点共同合作或产生关联,例如论文合作网,就往往涉及多个作者,或者一个人的观点,是受到多个人共同影响的。高阶网络考虑的就是多个节点间的连接,如下图所示: 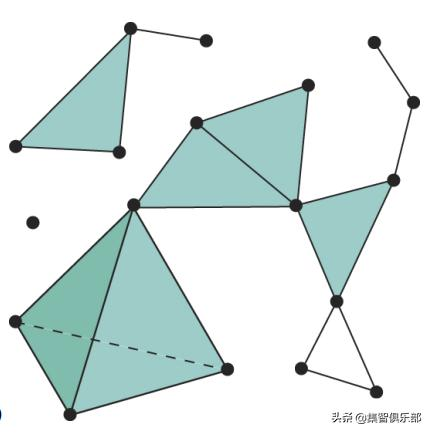 图 3:高阶网络示意图 对超图(hypergraph)的一种研究方法是将其用二分图(bipartite network)建模,即将节点分为A和B两类,A中的节点可以和多个B中的节点产生关联,但不会和A中的其他节点产生联系: 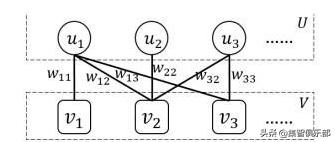 图 4:二分图示意图 鸟群的运动,是一种典型的涌现行为,每只鸟根据身边最近的几只鸟的运动来决定自己的飞行方向,由于同时受到多只鸟的影响,需要使用高阶网络进行建模,具体的模型称为拓扑数据分析(Topological Data Analysis),考察的是网络呈现出的性状,以及在不同维度下的结构洞。高阶网络的另一个研究套路是考察节点间的互动模式导致的相变(phase transition)和分叉(bifurcations)。  图 5:多层网络示意图 如果对高阶网络感兴趣:推荐下面的19年的综述型论文,该文关注一个节点位于多个网络的多层网络(multilayer network),如上图所示的交通图,自上而下,每层分别为火车地铁,公交。本文介绍了多层网络中与单层网络在建模时的不同之处,多层网络中的渗流与消息传播问题,并依次说明其在生物学,神经科学,交通建模,经济学,博弈论中的应用案例。 > 论文题目: Multilayer Networks in a Nutshell > > 论文地址: https://arxiv.org/abs/1804.03488 # **总结** 网络模型和分析过去在统计学,经济学,材料科学,气象学,人文科学等诸多领域都取得了显著的进展,未来随着在模型中引入时间,博弈和多元关系,必将能对更多的现象,进行更贴合实际的建模,预期会产出更丰盛的果实。 > 作者:郭瑞东 > > 审校:刘培源 > > 编辑:张爽